What Do the Angles of a Hexagon Add Up to
I am a former maths instructor and owner of DoingMaths. I love writing nearly maths, its applications and fun mathematical facts.
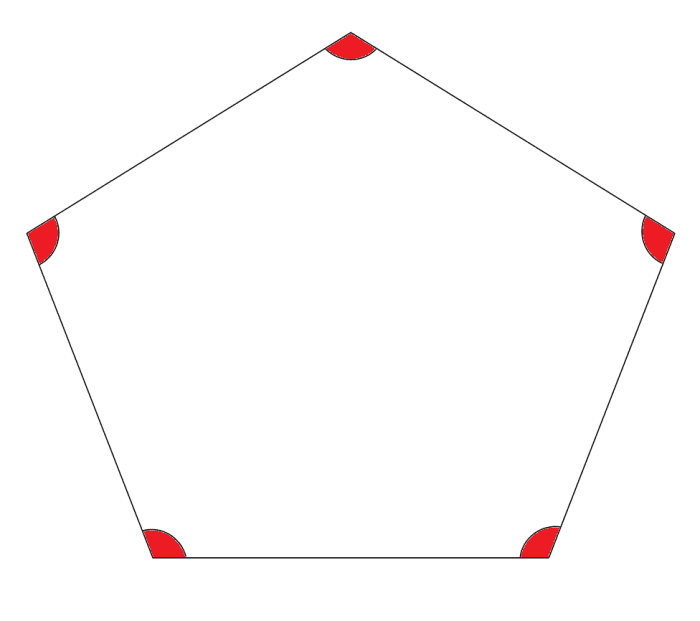
The interior angles of a pentagon.
My own picture
Angles on a Polygon
A polygon is any 2D shape constructed from a finite number of straight lines. For case; a triangle is a three-sided polygon, a square is a blazon of four-sided polygon and so on.
All of these polygons have angles both on the inside and and the outside, but what do these angles add up to? Do they e'er total the same matter? Is there a design to their totals? Permit's commencement by looking at the interior angles of a triangle.
The Sum of the Interior Angles of a Triangle
The interior angles of a polygon are, as the proper name suggests, the angles formed on the inside where the polygon's edges run across.
Before we commencement looking at the interior angles of many-sided polygons, nosotros will start with three-sided polygons, otherwise known every bit triangles.
We can apace piece of work out the sum of the iii interior angles of a triangle by because a triangle with an extra direct line fatigued parallel to the base of the triangle and touching the triangle'due south height corner equally in the diagram below.
To notice the sum of the interior angles a + b + c, we note that the bending ten, formed between the triangle and the parallel pinnacle line, is alternate to b, hence b = x. As well c = y. We can too see that x, a and y bring together together on the straight line, hence a + 10 + y = 180°.
Replacing x and y with b and c, we get that a + b + c = 180°. We have just shown that the three interior angles of a triangle must ever total 180°.
Proof of the Interior Bending Sum of a Triangle
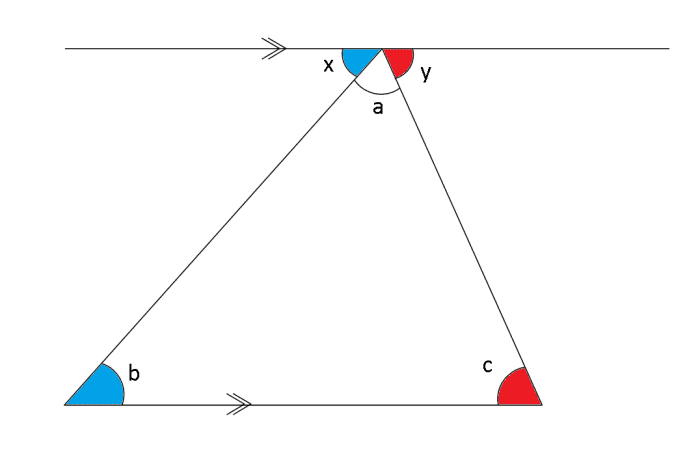
My own image
The Interior Angles of a Quadrilateral
A four-sided polygon is known as a quadrilateral. This group includes such familiar shapes as squares, rectangles, parallelograms and more than.
At present we know that a triangle'southward interior angles sum to 180°, we can apace calculate the sum of the quadrilateral'southward interior angles.
Take a await at the diagram beneath. We take taken a quadrilateral and divide information technology diagonally into two triangles. We tin run into from the diagram that the interior angles of the two triangles make upward all iv of the interior angles of the quadrilateral. Therefore the quadrilateral's angles must add upwards to twice that of the triangle'due south.
180° × 2 = 360° and so the interior angles of any quadrilateral must always equal 360°.
The Interior Angles of a Quadrilateral
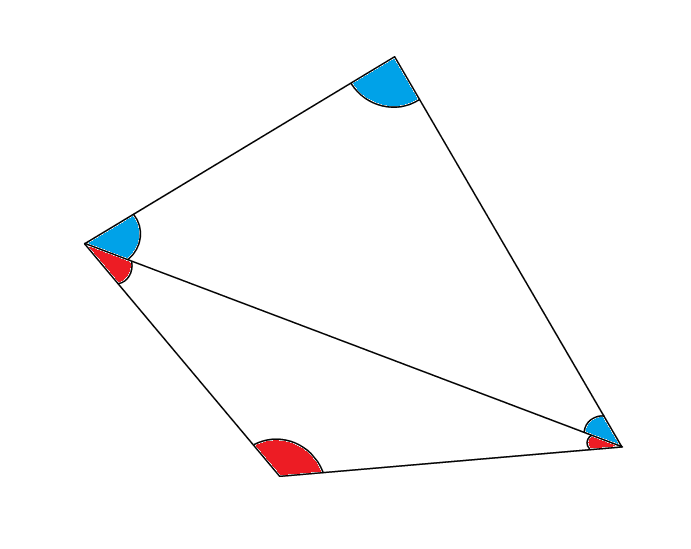
My ain image
Ringlet to Go along
Read More From Owlcation
The Interior Angles of Further Polygons
We tin apply this same method for calculating the interior angles of polygons with more iv sides. Simply cutting the polygon upward into triangles by using diagonal lines, making sure that the interior angles of the triangles all match up with the interior angles of the polygon. And then multiply the number of triangles by 180° to get the interior bending sum of the polygon.
The diagram below shows how this tin can be used on a pentagon (a five-sided polygon).
Interior Angles of a Pentagon
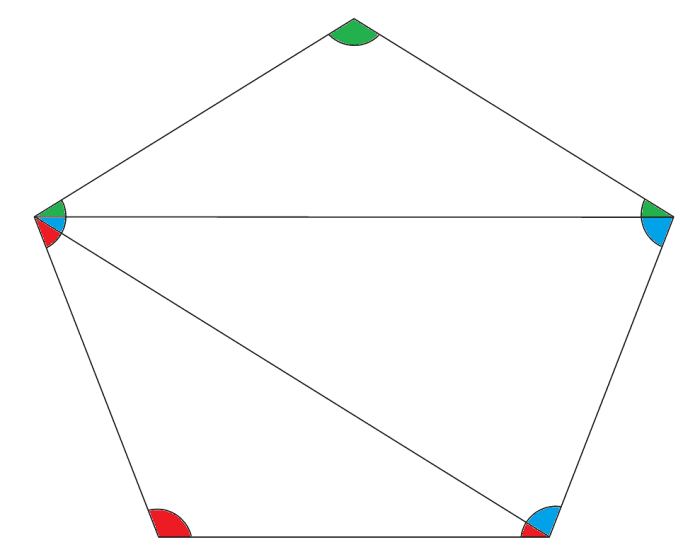
My ain image
The Interior Angle Sum of Further Polygons
Nosotros tin can see in the pentagon diagram that a pentagon is split up into 3 internal triangles then must have an interior bending sum of iii × 180° = 540°.
Information technology can be seen from our examples so far that the number of triangles that a polygon tin be split into is two fewer than the total number of sides. For example a four-sided quadrilateral is split into 4 − 2 = two triangles and a five-sided pentagon is split up into five − 2 = iii triangles.
Y'all can check quite chop-chop yourself that this can be expanded to cover further polygons. Whatever the number of sides, we minus two from this to give the number of triangles that we can carve up the polygon into. By multiplying this number of triangles by 180°, we so go the sum of the interior angles.
Interior Angle Sums of Various Polygons
| Polygon | Number of Sides | Number of Internal Triangles | Interior Angle Sum |
|---|---|---|---|
| Triangle | 3 | 1 | 180 |
| Quadrilateral | 4 | 2 | 360 |
| Pentagon | 5 | 3 | 540 |
| Hexagon | vi | 4 | 720 |
| Heptagon | 7 | 5 | 900 |
| Octagon | 8 | 6 | 1080 |
| Nonagon | 9 | vii | 1260 |
| Decagon | 10 | viii | 1440 |
| Icosagon | 20 | 18 | 3240 |
| northward-sided Polygon | north | northward - 2 | 180(n - 2) |
The General Formula
Equally we tin can always split the polygon into two fewer triangles than at that place are number of sides, a polygon with n sides can be split into n − 2 triangles and hence has an interior bending sum of 180(n − 2)°.
What Well-nigh Exterior Angles?
So far nosotros have been looking at the interior angles of a polygon, but what about exterior angles?
Exterior angles lie on the outside of the polygon and are created by extending a side and measuring the angle betwixt the extended side and the adjacent side. This tin can be seen in the diagram below.
Every bit the exterior angles are created by the extended straight line, an exterior bending and its corresponding interior angle must ever add together to make 180°.
Outside Angles of a Hexagon
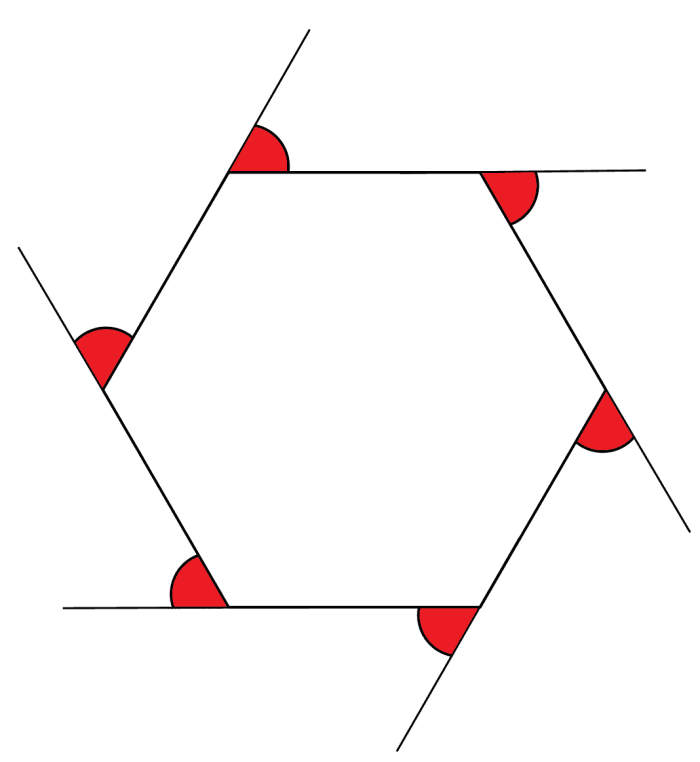
My own image
Computing the Sum of the Exterior Angles
To summate the sum of the exterior angles, imagine yous have a large polygon drawn on the floor and yous are walking forth a side. You reach the corner and then must rotate through the exterior bending in order to be facing along the next side. You walk along this second side and again when you reach the corner you lot rotate through the side by side exterior angle in order to continue your journeying.
This happens at each corner until you have returned to your starting signal. At this betoken you are at present facing the same management you started with having turned through a full circumvolve. A total circle is 360°, hence all of the exterior angles must sum to 360°.
This is the same regardless of how many sides the polygon has. The outside angles of a triangle add up to 360°; the outside angles of a decagon also add together upwards to 360°.
This content is authentic and true to the best of the writer's cognition and is not meant to substitute for formal and individualized advice from a qualified professional.
© 2021 David
David (author) from W Midlands, England on September 15, 2021:
You lot're welcome. Thanks for the squeamish comment.
Umesh Chandra Bhatt from Kharghar, Navi Mumbai, India on September xv, 2021:
Very nicely explained. Thanks.
Source: https://owlcation.com/stem/What-Do-The-Angles-In-a-Polygon-Add-Up-To
0 Response to "What Do the Angles of a Hexagon Add Up to"
Post a Comment